Logika Matematika

A. Pengertian Logika

Logika Matematika
Sumber Foto: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgFO_AUGrDuFrtELICnYZZFDaB3wEKVrfzT4oDdyPSdW8ZpkaixUD4HHrybU617UVAEejB33nOua5QDzkJyVoyjTju_qwm5FebRtbnPinydKWauhW7a_Ud3VhIJQY2o_qGEBmAsltZCZFM/s1600/images.png

Secara etimologi, istilah Logika berasal dari bahasa Yunani, yaitu logos yang berarti kata, ucapan, pikiran secara utuh, atau sanggup juga ilmu pengetahuan. Dalam arti luas, Logika yaitu sebuah metode dan prinsip-prinsip yang sanggup memisahkan secara tegas antara kebijaksanaan sehat yang sempurna dengan kebijaksanaan sehat yang tidak tepat.

Jika kita membahas logika, kita akan berkenalan dengan penalaran. Penalaran merupakan klarifikasi dalam upaya menunjukkan hubungan antara dua hal atau lebih menurut sifat-sifat atau hukum-hukum tertentu yang sudah diakui kebenarannya dengan langkah-langkah tertentu yang berakhir dengan sebuah kesimpulan. Dengan kata lain, kebijaksanaan sehat sanggup diartikan sebagai penarikan kesimpulan dalam sebuah argumen.

Dalam Logika, kita mempelajari dan meneliti apakah sebuah kebijaksanaan sehat yang telah kita lakukan itu sempurna atau tidak. Untuk sanggup berpikir dengan tepat, Logika menunjukkan sejumlah aturan atau kaidah-kaidah yang harus diperhatikan semoga kesimpulan yang kita peroleh akibatnya tepat.
         

Orang yang pertama kali merintis dan mempelopori Logika yaitu Aristoteles, seorang filsafat Yunani yang hidup pada 348-322 SM. Ia mengobservasi dan mencatat hukum-hukum dari logika formal, yaitu logika yang kesahihan dari langkah-langkahnya dipandang hanya menurut bentuk dari rangakaian langkah-langkah itu dan tidak bergantung pada bahan duduk kasus sehingga berlaku baik di ilmu alam, ilmu kimia, maupun ilmu-ilmu lain serta dalam kehidupan sehari-hari.

Contoh:
Premis 1 : Semua a yaitu b
Premis 2 : Semua b yaitu c
Kesimpulan : Semua a yaitu c
Langkah di atas menghasilkan sebuah kesimpulan yang tidak tergantung pada isi a, b dan c.

Dengan mempelajari Logika ini dibutuhkan kita memiliki pola berpikir yang tepat, akurat, rasional, kritis dan obyektif. Selain itu, dengan mempelajari prinsip-prinsip Logika, ini juga akan membantu kita untuk menjadi lebih efektif dalam mengenal dan menghindari kesalahan dalam penalaran, baik kebijaksanaan sehat yang dilakukan orang lain, maupun yang dilakukan oleh diri sendiri. Seseorang yang sanggup mengenal dan menghindari kesalahan logika dalam kebijaksanaan sehat akan sanggup berpikir yang terang dan tepat, lebih baik dan lebih yakin, apapun yang mungkin merupakan pokok duduk kasus yang akan dihadapi.

B. Himpunan Semesta Pembicaraan

Kenapa ada himpunan semesta pembicaraan ya? Bukannya kita kini sedang berguru Logika Matematika? Mungkin ada diantara kalian bertanya ibarat itu. Mungkin pada bahan di sekolah, hal ini kurang menerima perhatian. Karena ketika kita sedang membicarakan matematika, maka kita harus memilih terlebih dahulu himpunan semestanya, apalagi untuk Logika Matematika. Sebab benar atau salahnya suatu pernyataaan memang sanggup tergantung pada semestanya yang telah disepakati.

Contoh:

"Berapa x sehingga x + 2 = 12?"

Pasti kebanyakan kita akan menjawab x = 10.

Yap, benar. Anda tidak salah. Karena pikiran kita sudah terbentuk bahwa semesta pembicaraannya yaitu semua anggota himpunan bilangan kompleks.

Tapi lain balasan jikalau saya bertanya ibarat ini,

"Berapa x sehingga x + 1 = 12, dengan x yaitu anggota bilangan orisinil kurang dari 5?"

Jika Anda tahu, silahkan isi balasan dan alasannya di kolom komentar.

C. Kalimat = Pernyataan?

Apakah kalimat sanggup dikatakan pernyataan??? Faktanya tidak semua kalimat merupakan pernyataan, tetapi semua pernyataan merupakan sebuah kalimat. Suatu kalimat yang mengandung nilai benar ataupun salah, tetapi tidak kedua-duanya pada dikala yang sama disebut kalimat deklaratif (pernyataan). Kalimat yang tidak sanggup dinyatakan sebagai pernyataan sanggup berupa kalimat perintah, pertanyaan, kalimat yang tidak jelas, atau kalimat yang memiliki arti ganda (ambigu).

Contoh:

• Bilangan 7 yaitu bilangan prima.
• Provinsi DKI Jakarta berpenduduk 1 juta jiwa.
• Ambilkan OHP di ruang guru!
• Astaga!
• 2x + 3 > x -1

Dari teladan di atas, kalimat pertama dan kedua yaitu teladan pernyataan, dan kalimat lainnya merupakan kalimat biasa. Untuk kalimat kelima tidak disebut sebagai sebuah pernyataan alasannya yaitu belum sanggup ditentukan nilai kebenarannya. Kalimat yang masih mengandung variabel sanggup disebut sebagai kalimat terbuka (bisa dimasukkan apa saja). Kalimat tersebut akan menjadi sebuah pernyataan jikalau kita telah mengganti nilai x dengan suatu bilangan tertentu. Saya kira hingga disini Anda sudah paham perbedaan kalimat dan pernyataan.

D. Operasi pada Logika Matematika

Secara umum, operasi pada bahan Logika matematika ada dua, yaitu operasi uner dan operasi biner. Sesuai namanya, operasi uner (Monari) yaitu operasi yang hanya berafiliasi dengan satu unsur, sedangkan operasi biner (Binari) yaitu operasi yang berafiliasi dengan dua unsur. Operasi uner dalam Logika Matematika hanya ada satu macam, yaitu operasi negasi, dan operasi biner ada empat macam, yaitu operasi konjungsi, disjungsi, implikasi, biimplikasi.

1) Operasi Negasi

Negasi biasa juga disebut dengan ingkaran. Nilai kebenaran negasi sebuah pernyataan yaitu kebalikan dari nilai kebenaran yang dimiliki oleh sebuah pernyataan. Jika sebuah pernyataan itu bernilai benar, maka negasinya yaitu salah, dan begitu pula sebaliknya. Untuk menyatakan negasi, kita sanggup memakai kata "tidak".

Tabel Nilai Kebenaran Operasi Negasi

Contoh:

"Pohon ini tinggi"

Pohon ini tinggi sanggup disimbolkan dengan p, negasinya sanggup disimbolkan dengan 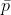atau 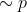sehingga pernyataan negasinya menjadi,

"Pohon ini tidak tinggi" atau sanggup juga, "Tidak benar bahwa pohon ini tinggi"

2) Operasi Konjungsi

Dalam Logika Matematika, jikalau dua pernyataan digabungkan dengan kata penghubung "dan", maka ini disebut sebagai operasi konjungsi. Simbol yang umum dipakai untuk operasi ini yaitu ""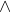

Tabel Nilai Kebenaran Operasi Konjungsi

Kesimpulan : Operasi konjungsi bernilai benar apabila kedua pernyataan tersebut bernilai benar.

Contoh:

• 2 yaitu bilangan prima genap dan 5 yaitu bilangan prima ganjil, bernilai benar
• 2 yaitu bilangan prima genap dan 5 yaitu bukan bilangan prima ganjil, bernilai salah
• 2 yaitu bukan bilangan prima genap dan 5 yaitu bilangan prima ganjil, bernilai salah
• 2 yaitu bukan bilangan prima genap dan 5 yaitu bukan bilangan prima ganjil, bernilai salah

3) Operasi Disjungsi

Jika dua pernyataan digabungkan dengan kata penghubung "atau", maka ini disebut sebagai operasi disjungsi. Simbol yang umum dipakai untuk operasi ini yaitu ""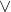

Tabel Nilai Kebenaran Operasi Disjungsi

Kesimpulan : Operasi disjungsi bernilai benar apabila salah satu pernyataan tersebut bernilai benar.

Contoh:

• 2 yaitu bilangan genap atau 2 yaitu bilangan prima, bernilai benar
• 2 yaitu bilangan genap atau 2 yaitu bukan bilangan prima, tetap bernilai benar
• 2 yaitu bukan bilangan genap atau 2 yaitu bilangan prima, tetap bernilai benar
• 2 yaitu bukan bilangan genap atau 2 yaitu bilangan prima, gres bernilai salah

4) Operasi Implikasi

Jika dua pernyataan mengandung bentuk "jika ... maka ...", maka ini disebut sebagai operasi implikasi. Simbol yang umum dipakai untuk menyatakan operasi ini yaitu "".

Tabel Nilai Kebenaran Operasi Implikasi

Kesimpulan : Operasi implikasi bernilai benar apabila pernyataan kedua bernilai benar, atau kedua pernyataan tersebut bernilai sama.

Contoh:

• Jika air habis, maka insan akan mati, bernilai benar
• Jika air habis, maka insan tidak akan mati, bernilai salah
• Jika air tidak habis, maka insan akan mati, bernilai benar
• Jika air tidak habis, maka insan tidak akan mati, bernilai benar

Contoh di atas saya rasa sudah cukup untuk menjawab pertanyaan "Kenapa jikalau B maka S akibatnya S, sedangkan jikalau S maka B akibatnya B?" Karena belum tentu penyebab insan mati hanya alasannya yaitu air habis, kan?

5) Operasi Biimplikasi

Jika dua pernyataan mengandung bentuk " ... jikalau dan hanya jikalau ...", maka ini disebut sebagai operasi biimplikasi. Saya lebih suka menyebut hubungan ini "persyaratan". Simbol yang umum dipakai untuk operasi ini yaitu "".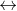

Tabel Nilai Kebenaran Operasi Biimplikasi

Kesimpulan : Operasi biimplikasi bernilai benar apabila kedua pernyataan tersebut bernilai sama.

Contoh:

• Jantung berdetak jikalau dan hanya jikalau insan hidup, bernilai benar
• Jantung berdetak jikalau dan hanya jikalau insan tidak hidup, ya salah kan?
• Jantung tidak berdetak jikalau dan hanya jikalau insan hidup, salah juga kan?
• Jantung tidak berdetak jikalau dan hanya jikalau insan tidak hidup, gres benar

Syarat insan hidup yaitu jantung berdetak, dan syarat jantung berdetak yaitu insan hidup. Kedua hal tersebut tidak sanggup dipisahkan satu sama lain. Inilah yang saya maksud dengan hubungan "persyaratan".

6) Konvers

Konvers yaitu kebalikan dari implikasi ditandai dengan pertukaran letak. 

Misal implikasi p → q, maka konversnya yaitu q → p.

7) Invers

Invers merupakan lawan dari implikasi. Pada invers, pernyataan yang terdapat dalam pernyataan beragam merupakan negasi dari pernyataan pada implikasi.

Misal implikasi p → q, maka inversnya yaitu p → q.

8) Kontraposisi

Kontraposisi merupakan kebalikan dari invers sama halnya dengan konvers hanya saja pernyataannya merupakan negasi atau ingkaran. 

Misal invers p → q, maka kontraposisinya yaitu q → p.

E. Kesetaraan

Kesetaraan merupakan pernyataan-pernyataan yang bernilai sama atau bermakna sama. Kesetaraan dilambangkan dengan " ≡ ".

1. (p ∧ q) ≡ p ∨ q

2. (p ∨ q) ≡ p ∧ q

3. p → q ≡ q → p

4. (p → q) ≡ (p ∧ q)

5. (p ↔ q) ≡ (p ∧ q) ∨ (q ∧ p) 

F. Pernyataan Berkuantor

Seperti yang sudah dibahas, 2x + 3 > x -1 yaitu kalimat terbuka (yang mengandung variabel) dan bukan sebuah pernyataan. Untuk mengganti kalimat terbuka tersebut menjadi sebuah pernyataan, kita harus mengganti variabel (x) yang ada dengan suatu nilai. Cara lainnya untuk mengganti kalimat terbuka menjadi sebuah pernyataan yaitu dengan memakai kuantor. Kuantor sendiri dibagi menjadi dua, yaitu kuantor umum (kuantor universal) dan kuantor khusus (kuantor eksistensial).

1) Kuantor Umum (Kuantor Universal)

Untuk menyatakan kuantor universal, kita sanggup memakai ungkapan "Untuk setiap" atau "Untuk semua". Simbol yang umum dipakai untuk menyatakan kuantor umum yaitu A terbalik, "".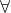

Contoh:

x > 0 merupakan kalimat terbuka.

Jika saya ganti menjadi "Untuk setiap x bilangan asli, berlaku x positif (x >0)", apakah sanggup kita menyatakan salah atau benar? Bisa, bukan? Jawabannya yaitu benar alasannya yaitu 1, 2, 3 dst itu selalu lebih besar dari 0. Dan jikalau sanggup ada nilai kebenarannya, maka ini disebut sebagai pernyataan. Simbol matematikanya adalah

Untuk teladan pernyataan berkuantor universal yang bernilai salah sanggup dilihat apabila saya ganti pernyataannya dengan, "Untuk setiap x bilangan asli, x > 2". Kenapa salah? Karena 1 yaitu bilangan asli, sedangkan 1 tidak lebih besar daripada 2. Jadi, tidak semua bilangan orisinil lebih dari 2 dan sanggup disimpulkan bahwa pernyataan tersebut bernilai salah.

2) Kuantor Khusus (Kuantor Eksistensial)

Untuk menyatakan kuantor khusus, kita sanggup memakai ungkapan "Ada", "Terdapat", "Paling sedikit satu", atau "Beberapa". Simbol yang umum dipakai untuk menyatakan kuantor khusus yaitu E terbalik, ""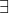

Contoh:

x > 1 merupakan kalimat terbuka

Jika saya ganti menjadi "Terdapat x bilangan orisinil sedemikian sehingga x > 1", apakah sanggup kita menyatakan salah atau benar? Sekali lagi bisa. Dan jawabannya benar alasannya yaitu 2 > 1 sedangkan 2 yaitu anggota bilangan asli. Kaprikornus ini sanggup disebut sebagai suatu pernyataan. Simbol matematikanya yaitu

Untuk teladan pernyataan berkuantor eksistensial yang bernilai salah sanggup dilihat apabila saya ganti pernyataannya dengan, "Terdapat x bilangan orisinil sedemikian rupa sehingga x < 1". Kenapa salah? Karena tidak ada lagi bilangan orisinil yang lebih kecil dari 1. Jadi, tidak terdapat bilangan orisinil yang kurang dari 1 dan sanggup disimpulkan bahwa pernyataan tersebut bernilai salah.

G. Negasi Pernyataan Berkuantor

Coba kita melihat pernyataan ini, "Semua insan niscaya mati". Pernyataaan ini bernilai benar.

Negasi dari pernyataan ini yaitu "Tidak semua insan niscaya mati", ini sama artinya dengan "Terdapat insan yang tidak niscaya mati". Dan pernyataan ini bernilai salah. Jadi, kita sanggup menyimpulkan bahwa negasi yang telah kita buat sudah benar.

Simbol Matematis Negasi Kuantor Universal

Sekarang coba lihat pernyataan ini, "Terdapat tinggi tubuh insan yang kurang dari 120 cm". Pernyataan ini bernilai benar.

Negasi dari pernyataan ini yaitu "Tidak terdapat tinggi tubuh insan yang kurang dari 120 cm", ini sama artinya dengan "Semua tinggi tubuh insan lebih dari 120 cm". Dan pernyataan ini bernilai salah. Jadi, kita sanggup menyimpulkan bahwa negasi yang telah kita buat sudah benar.

Simbol Matematis Negasi Kuantor Eksistensial

Kesimpulan : (1) Negasi universal = eksistensial; dan (2) Negasi eksistensial = universal

H. Penarikan Kesimpulan

1. Modus Ponens

p → q

p

————

∴ q

Contoh:

Diketahui pernyataan sebagai berikut:

1. Jika hari libur tiba, maka Rani akan berlibur ke Paris

2. Hari libur datang

Tentukan kesimpulan yang sah dari dua pernyataan tersebut.

Pembahasan:

Misalkan:

p = Hari libur tiba

q = Rani berlibur ke Paris

Berdasarkan modus Ponens, diperoleh :

p → q

p

———

∴ q

Jadi, kesimpulan yang sah yaitu Rani berlibur ke Paris

2. Modus Tollens

p → q

q

————

∴ p

Contoh :

Diketahui pernyataan sebagi berikut:

1. Jika hari ini hujan, maka Lia tidak pergi ke kota

2. Lia pergi ke kota

Tentukan kesimpulan yang sah dari dua pernyataan tersebut.

Pembahasan

Misalkan :

p = Hari ini hujan

q = Lia tidak pergi ke kota

q = Lia pergi ke kota

Berdasarkan Modus Tollens diperoleh :

p → q

q

————

∴ p

Jadi, kesimpulan yang sah yaitu Hari ini tidak hujan.

3. Silogisme 

p → q

q → r

————

∴ p → r

Contoh :

Diketahui pernyataan sebagi berikut :

1. Jika Tio menjadi juara kelas, maka Ibu akan membelikannya sepeda

2. Jika Ibu membelikannya sepeda, maka Tio akan bahagia

Tentukan kesimpulan yang sah dari dua pernyataan tersebut.

Pembahasan :

Misalkan :

p = Tio menjadi juara kelas

q = Ibu membelikannya sepeda

r = Tio bahagia

Berdasarkan konsep silogisme diperoleh :

p → q

q → r

————

∴ p → r

Jadi, kesimpulan yang sah yaitu Jika Tio menjadi juara kelas, maka Tio akan senang.

Sumber:

aciknadzirah.blogspot.com/search?q=logika-matematika

Sumber http://gurumatiksma.blogspot.com

Share this post

Berlangganan update artikel terbaru via email: