Pengertian Serta Teladan Bilangan Bundar Aktual Dan Negatif

Bilangan bundar ialah sistem bilangan yang merupakan himpunan dari semua bilangan (bukan pecahan) yang terdiri dari bilangan bulat negatif {…,-3,-2,-1}, nol {0}, dan bilangan bulat positif {1,2,3,…}. Bilangan bundar merupakan himpunan bab dari bilangan rasional.

Contoh bilangan bundar positif: 133, 45, 31, 1000

Contoh bilangan bundar negatif: -121, -7, -8, -9, -111

Contoh bukan bilangan bulat: -3½

Baca juga: Pengertian Matematika dan Terapannya dalam Kehidupan

A. Penyusun Bilangan Bulat

Himpunan semua bilangan bundar dalam ilmu matematika dilambangkan dengan ℤ atau “Zahlen” (bahasa jerman yang berarti bilangan).

ℤ = Himpunan bilangan bulat

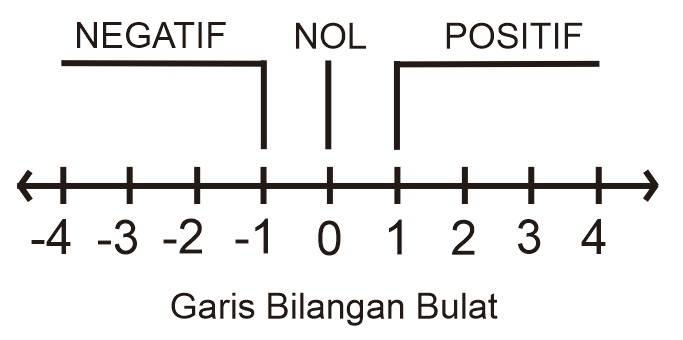
Berikut bilangan bundar pada garis bilangan:

• Bilangan Bulat Negatif

  Bilangan bundar negatif ialah semua bilangan bundar di sebelah kiri garis bilangan yang dibatasi oleh angka nol. Misalnya: -4, -3, -2, -1

• Angka Nol

  Angka nol ialah digit yang memainkan peranan penting dalam ilmu matematika. Dalam operasi penjumlahan, angka nol menjadi unsur identitas. Ini artinya setiap angka yang dijumlahkan dengan angka nol menghasilkan angka itu sendiri.

• Bilangan Bulat Positif atau Bilangan Asli

  Bilangan bundar kasatmata ialah semua bilangan bundar di sebelah kanan garis bilangan yang dibatasi oleh angka nol. Misalnya: 1, 2, 3, 4, dst. Bilangan bundar kasatmata dibagi menjadi 2, yaitu bilangan ganjil dan bilangan genap.

  • Bilangan Ganjil

    Bilangan ganjil ialah bilangan bundar kasatmata yang tidak habis dibagi 2. Misalnya: 1, 3, 5, 7, dst.

  • Bilangan Genap

    Bilangan genap ialah bilangan bundar kasatmata yang habis dibagi 2. Misalnya: 2, 4, 6, dst.

Catatan: Nol dan bilangan orisinil membentuk sistem bilangan cacah, {0, 1, 2, 3, …}.

---

B. Sifat-Sifat Bilangan Bulat

Berikut sifat-sifat bilangan bulat:

Sifat	Penambahan	Perkalian
Tertutup	a + b = ialah bilangan bulat	a × b = ialah bilangan bulat
Asosiatif	a + (b + c)  =  (a + b) + c	a × (b × c)  =  (a × b) × c
Komutatif	a + b  =  b + a	a × b  =  b × a
Mempunyai unsur identitas	a + 0  =  a	a × 1  =  a
Setiap bilangan punya invers	a + (−a)  =  0	Tidak punya
Distributif	a × (b + c)  =  (a × b) + (a × c)
Tidak ada pembagi nol	–	jika a × b = 0, maka a = 0 atau b = 0 (atau keduanya)

Keterangan:

Tertutup: operasi perkalian dan penjumlahan bilangan bundar menghasilkan bilangan bulat.

Tidak ada pembagi nol: pembagian bilangan bundar dengan nol menghasilkan nilai tidak terdefinisi (∞).

Asosiatif: penjumlahan atau perkalian tiga buah bilangan bundar yang dikelompokkan secara berbeda memiliki hasil yang sama.

Komutatif: pertukaran letak angka pada penjumlahan dan perkalian bilangan bundar memiliki hasil sama.

Contoh:

1 + 2 = 2 + 1
3 × 4 = 4 × 3

Unsur identitas: operasi perkalian dan penjumlahan setiap bilangan bundar dengan identitasnya sanggup menghasilkan bilangan itu sendiri

• Identitas Penjumlahan (0), 7 + 0 = 7
• Identitas Perkalian (1), 2 × 1 = 2

Mempunyai Invers: setiap bilangan bundar memiliki invers terhadap operasi penjumlahan, suatu bilangan bundar yang dioperasikan dengan inversnya menghasilkan unsur identitas penjumlahan.

Contoh:

-7 + 7 = 0; 0 ialah unsur identitas penjumlahan, jadi 7 invers penjumlahannya -7

Sifat Distributif: suatu penggabungan dengan cara mengkombinasikan bilangan dari hasil operasi terhadap elemen-elemen kombinasi tersebut

---

 C. Dasar Bahasa Pemrograman Komputer

Di bidang ilmu komputer, bilangan bundar menjadi salah satu tipe data dasar untuk menulis program. Dalam hal ini, bilangan bundar lebih dikenal dengan nama integer.

Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika

---

Sekian artikel Pengertian serta Contoh Bilangan Bulat. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…

Sumber https://www.advernesia.com/

Share this post

Berlangganan update artikel terbaru via email: