Pengertian Bilangan Rasional Dan Irasional Serta Contohnya
Bilangan rasional dan irasional merupakan 2 jenis bilangan yang merupakan cuilan dari sistem bilangan real (R).
Artikel terkait: Bilangan Real | Pengertian Bilangan Real dan Contohnya
A. Pengertian Bilangan Rasional (Q)
Bilangan rasional yakni sistem bilangan yang merupakan himpunan dari semua bilangan yang sanggup dinyatakan dalam bentuk pecahan a/b dengan a, b yakni bilangan bundar dan b ≠ 0. Secara mendasar bilangan rasional berasal dari bahasa inggris yaitu “rational” lantaran bilangan ini sanggup dinyatakan dalam bentuk perbandingan (rasio). Ahli matematika memperlihatkan simbol Q untuk bilangan rasional.
Artikel terkait: Pengertian serta Contoh Bilangan Bulat Positif dan Negatif
Misalnya:
Bilangan 1,2 termasuk bilangan rasional, lantaran sanggup dinyatakan dalam bentuk pecahan berikut
1,2 sanggup dinyatakan dalam bentuk pecahan 12/10, 6/5, ataupun bentuk pecahan lain yang memenuhi a/b dengan a,b (bilangan bulat) dan b ≠ 0. Sehingga 1,2 termasuk bilangan rasional.
Contoh Bilangan Rasional
| Bilangan | a/b | Rasional |
|---|---|---|
| 0 | 0/1 | Ya |
| 1,2 | 6/5 | Ya |
| 4 | 4/1 | Ya |
| 0,45 | 45/100 | Ya |
| √3 | (tidak ada) | Tidak |
| 30% | 30/100 | Ya |
Sifat-Sifat Bilangan Rasional
Bilangan rasional sanggup didefinisikan untuk setiap 
merupakan bilangan rasional dalam bentuk pecahan, maka berlaku sifat-sifat berikut:
-
Tertutup, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional juga menghasilkan bilangan rasional.
menghasilkan bilangan rasional.
menghasilkan bilangan rasional. -
Komutatif, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional memiliki sifat komutatif, yang sanggup dirumuskan sebagai berikut,
-
Asosiatif, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional memiliki sifat asosiatif, yang sanggup dirumuskan sebagai berikut,
-
Distributif
Bilangan rasional memiliki sifat distributif, yang sanggup dirumuskan sebagai berikut,
-
Punya elemen identitas penjumlahan dan perkalian
-
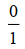adalah elemen identitas penjumlahan bilangan rasional, lantaran setiap x bilangan rasional yang dijumlahkan dengan 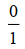karenanya yakni x bilangan rasional itu sendiri.
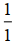adalah elemen identitas perkalian bilangan rasional, lantaran setiap x bilangan rasional yang dikalikan dengan 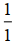karenanya x bilangan rasional itu sendiri.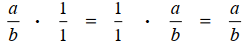
-
-
Setiap elemen punya invers terhadap operasi penjumlahan dan perkalian
Setiap bilangan rasional memiliki elemen invers terhadap operasi penjumlahan dan perkalian. Sehingga setiap bilangan rasional yang dioperasikan dengan invers menghasilkan elemen identitas.
adalah invers penjumlahan untuk setiap bilangan rasional 
, sehingga berlaku 
adalah invers perkalian untuk setiap bilangan rasional ≠ 0, sehingga berlaku 
-
Perkalian dengan Nol (0)
Perkalian bilangan rasional dengan angka nol menghasilkan angka nol, sehingga berlaku
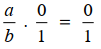
B. Pengertian Bilangan Irasional
Bilangan irasional yakni sistem bilangan yang tidak sanggup dinyatakan dalam bentuk pecahan a/b dengan a, b yakni bilangan bundar dan b ≠ 0, namun sanggup dinyatakan dalam bentuk desimal.
Contoh Bilangan Irasional dan Penjelasannya
| Bilangan | a/b | irasional |
|---|---|---|
| √2 = 1,4142 … | Tidak ada | Ya |
| √3 = 1,7320 … | Tidak ada | Ya |
| √4 = 2 | 2/1 | Tidak |
| Ï€ = 3,14159 … | Mendekati 22/7 | Ya |
| e = 2,71828 … | Tidak ada | Ya |
| 0,25 | 1/4 | Tidak |
Sifat-Sifat Bilangan Irasional
Secara umum bilangan rasional dan irasional memiliki sifat yang hampir sama yaitu komutatif, asosiatif, distributif, memiliki elemen identitas, setiap elemen punya invers, dan perkalian dengan 0. Satu sifat yang berbeda yakni bilangan irasional bersifat tidak tertutup.
Sifat tidak tertutup
Sifat tidak tertutup pada bilangan irasional disebabkan lantaran operasi penjumlahan dan perkalian antar bilangan irasional dapat menghasilkan bilangan rasional.
Contoh:
√2 × √2 = √4 = 2; hasil rasional
√2 × √3 = √6; hasil tetap irasional
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Pengertian Bilangan Rasional dan Irasional serta Contohnya“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…
Sumber https://www.advernesia.com/
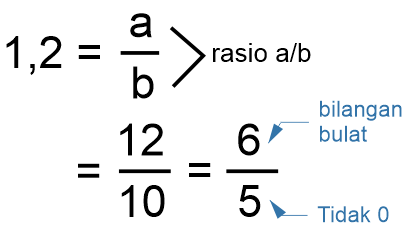
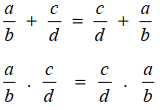
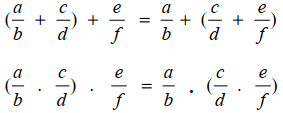
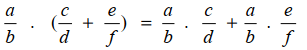
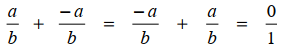
0 Response to "Pengertian Bilangan Rasional Dan Irasional Serta Contohnya"
Posting Komentar