Rumus Balok | Rumus Volume Balok Dan Rumus Luas Permukaan Balok
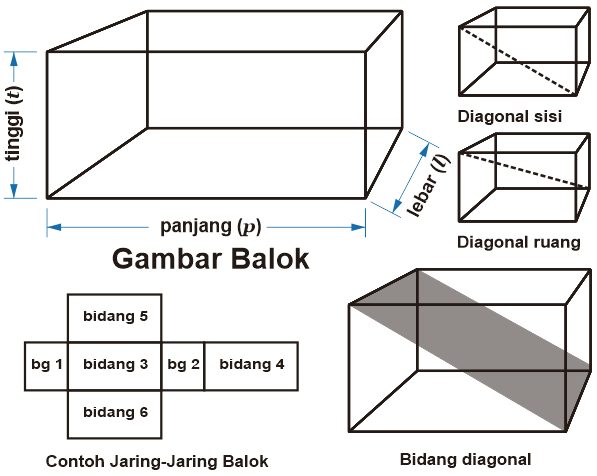
A. Pengertian Balok atau Cuboid
Balok yaitu bangkit ruang tiga dimensi yang tersusun oleh 3 pasang segi empat (persegi atau persegi panjang) dan paling sedikit memiliki 1 pasangan sisi segi empat yang memiliki bentuk yang berbeda. Sebelum mempelajari rumus volume balok dan luas permukaan balok, sebaiknya kita memahami sifat-sifat balok, bagian-bagian balok, dan jaring-jaring balok.
Artikel terkait: Rumus Kubus | Volume Kubus dan Luas Permukaan Kubus
B. Sifat-Sifat Balok, Bagian Balok, dan Jaring-Jaring Balok
Berikut sifat-sifat umum balok:
- Balok tersusun dari 3 pasang sisi yang sama (total 6 buah sisi).
- Setiap sisi berbentuk segiempat yaitu persegi atau persegi panjang.
- Paling sedikit harus memiliki 1 pasang sisi dengan bentuk yang berbeda.
- Mempunyai 12 rusuk.
- Rusuk-rusuk yang sejajar memiliki ukuran yang sama.
- Mempunyai 4 diagonal bidang.
- Diagonal bidang yang sejajar memiliki ukuran yang sama.
- Mempunyai 4 diagonal ruang dan semuanya memiliki ukuran yang sama.
- Setiap bidang diagonal berbentuk persegi panjang.
C. Rumus Balok
t = tinggi, p = panjang, l = lebar
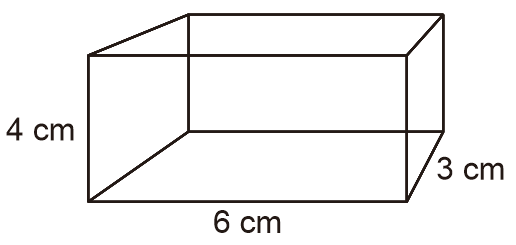
Contoh 1: Menghitung Volume dan Luas Permukaan Balok
Hitunglah volume dan luas permukaan balok berikut!
Diketahui:
p = 6 cm
l = 3 cm
t = 4 cm
Ditanya:
Volume (V) dan Luas Permukaan (L) Balok
Penyelesaian:
V = p × l × t
V = 6 cm × 3 cm × 4 cm
V = 72 cm³
L = 2 × (p.l + p.t +l.t)
L = 2 × ((6 cm × 3 cm) + (6 cm × 4 cm) + (3 cm × 4 cm))
L = 2 × (18 cm² + 24 cm² + 12²)
L = 2 × 54 cm²
L = 108 cm²
Jadi, volume balok yaitu 72 cm³ dan luas permukaan balok yaitu 108 cm².
Contoh 2: Cara Menghitung Panjang Balok Jika Diketahui Luas Permukaannya
Sebuah balok memiliki luas permukaan 52 cm², kalau diketahui lebar balok 2 cm dan tinggi balok 3 cm. Hitunglah panjang balok tersebut!
Diketahui:
L = 52 cm²
l = 2 cm
t = 3 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
Jadi, panjang balok yaitu 5 cm.
Contoh 3: Cara Menghitung Panjang Balok Jika Diketahui Volume
Sebuah balok memiliki volume 12 cm³, kalau diketahui lebar balok 2 cm dan tinggi balok 2 cm. Hitunglah panjang balok tersebut!
Diketahui:
V = 12 cm³
l = 2 cm
t = 2 cm
Ditanya:
Panjang balok (p)
Penyelesaian:
p = V ÷ l ÷ t
p = 12 cm³ ÷ 2 cm ÷ 2 cm
p = 3 cm
Jadi, panjang balok yaitu 3 cm.
Contoh 4: Cara Menghitung Lebar Balok Jika Diketahui Luas Permukaannya
Sebuah balok memiliki luas permukaan 214 cm², kalau diketahui panjang balok 7 cm dan tinggi balok 5 cm. Hitunglah lebar balok tersebut!
Diketahui:
L = 214 cm²
p = 7 cm
t = 5 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
Jadi, lebar balok yaitu 6 cm.
Contoh 5: Cara Menghitung Lebar Balok Jika Diketahui Volume
Sebuah balok memiliki volume 336 cm³, kalau diketahui panjang balok 8 cm dan tinggi balok 6 cm. Hitunglah lebar balok tersebut!
Diketahui:
V = 336 cm³
p = 8 cm
t = 6 cm
Ditanya:
Lebar balok (l)
Penyelesaian:
l = V ÷ p ÷ t
l = 336 cm³ ÷ 8 cm ÷ 6 cm
l = 7 cm
Jadi, panjang lebar yaitu 7 cm.
Contoh 6: Cara Menghitung Tinggi Balok Jika Diketahui Luas Permukaannya
Sebuah balok memiliki luas permukaan 382 cm², kalau diketahui panjang balok 9 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
L = 382 cm²
p = 9 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
Jadi, tinggi balok yaitu 7 cm.
Contoh 7: Cara Menghitung Tinggi Balok Jika Diketahui Volume
Sebuah balok memiliki volume 7120 cm³, kalau diketahui panjang balok 10 cm dan lebar balok 8 cm. Hitunglah tinggi balok tersebut!
Diketahui:
V = 720 cm³
p = 10 cm
l = 8 cm
Ditanya:
Tinggi balok (l)
Penyelesaian:
l = V ÷ p ÷ l
l = 720 cm³ ÷ 10 cm ÷ 8 cm
l = 9 cm
Jadi, panjang lebar yaitu 9 cm.
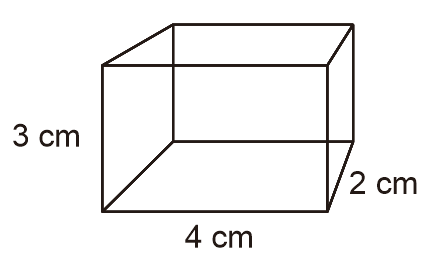
Contoh 8: Menghitung Diagonal Bidang, Diagonal Ruang, dan Luas Bidang Diagonal
Hitunglah panjang diagonal bidang, diagonal ruang, dan luas bidang diagonal balok di bawah!
Diketahui:
p = 4 cm
l = 2 cm
t = 3 cm
Penyelesaian:
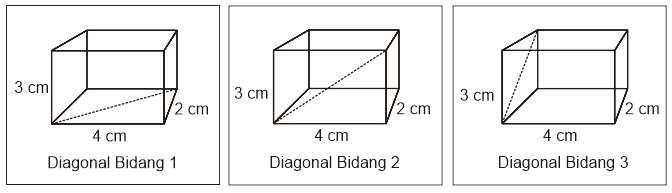
Panjang diagonal bidang
Balok memiliki 12 diagonal bidang dan dibagi menjadi 3 kelompok diagonal bidang
Dengan panjang masing-masing, sanggup dihitung memakai rumus Pythagoras
Artikel terkait: Rumus Pythagoras Segitiga dan Contoh Soalnya
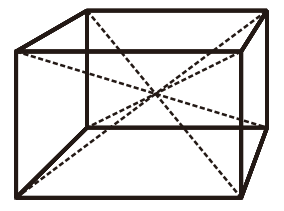
Panjang diagonal ruang
Balok memiliki 4 diagonal ruang yang sama panjang
Dengan panjang setiap diagonal ruang
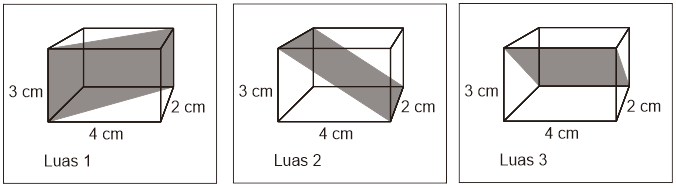
Luas bidang diagonal
Balok memiliki 3 pasangan luas bidang diagonal (total 6 bidang diagonal):
Dengan luas setiap bidang diagonal
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Pierce, Rod. “Maths is Fun – Privacy Statement” Math Is Fun. Ed. Rod Pierce. 10 Mar 2019. 30 Mar 2019 <https://www.mathsisfun.com/Privacy.htm>
Sekian artikel “Rumus Volume Balok dan Rumus Luas Permukaan Balok”. Nantikan artikel menarik lainnya dan mohon untuk share dan juga menyukai Fans Page Advernesia. Terima kasih…
Sumber https://www.advernesia.com/
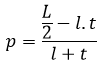
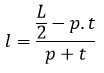
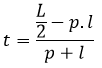
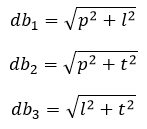
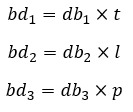
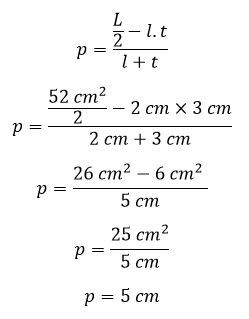
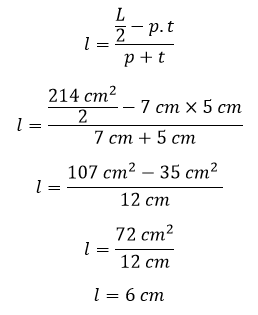
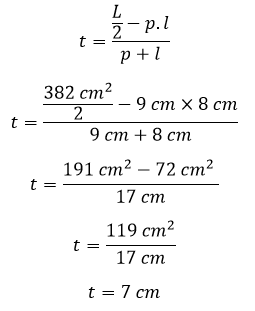
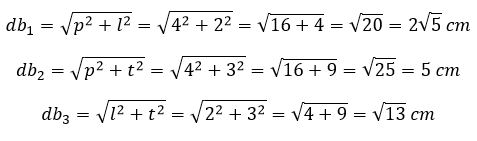
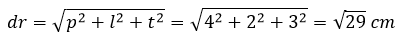
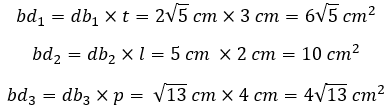
0 Response to "Rumus Balok | Rumus Volume Balok Dan Rumus Luas Permukaan Balok"
Posting Komentar