Bentuk Pangkat, Akar Dan Logaritma
A. Bentuk Pangkat (Eksponen)
1. Pangkat Bulat Positif
>>
>>
>>
>>
>>
b) Notasi Ilmiah
Bilangan besar yaitu bilangan yang nilainya lebih dari 10. Notasi ilmiahnya sanggup dinyatakan sebagai :
>>
2. Pangkat Bulat Negatif
Notasi ilmiah bilangan kecil yaitu bilangan yang berkisar antara 0 - 1, dinyatakan sebagai :
>>
>>
B. Bentuk Akar
1. Bilangan Rasional
Himpunan Bilangan Rasional yaitu himpunan yang anggotanya mempunyai sifat m/n, dengan m anggota bilangan lingkaran dan n anggota bilangan asli. Ada dua kemungkinan yang sanggup terjadi :
- Jika m habis dibagi dengan n, maka m/n yaitu bilangan bulat
- Jika m tidak habis dibagi dengan n, maka m/n yaitu bilangan pecahan
>>
3. Bilangan Irasional
Bilangan irasional yaitu suatu bilangan yang tidak sanggup dibagi alasannya yaitu hasil baginya tidak akan pernah terhenti. Kaprikornus pada intinya, kalau bilangan tersebut tidak sanggup dijadikan bentu a/b maka merupakan bilangan irasional. Contoh : 
.
4. Bentuk Akar
Jika n bilangan asli dengan n > 1 dan n Є R, maka akar pangkat n bilangan a ditulis: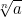
,
didefinisikan sebagai berikut:
>>
.4. Bentuk Akar
Jika n bilangan asli dengan n > 1 dan n Є R, maka akar pangkat n bilangan a ditulis:
, didefinisikan sebagai berikut:
>>
>>
5. Menyederhanakan Bentuk Akar
>>1.
>>2.
>>3.
dimana p < n dan q < n.>>4.
>>5.
>>6.
>>7.
6. Operasi Aljabar pada Bentuk Akar
a) Penjumlahan dan Pengurangan Bentuk Akar
Ingat, operasi aljabar sanggup dilakukan apabila akar-akarnya sejenis!!!
1)
2)
b) Perkalian Bentuk Akar
Ingat, operasi aljabar sanggup dilakukan apabila akar pangkatnya sama!!!
1)
2)
3)
4)
c) Menyederhanakan Bentuk
>>
>>
7. Merasionalkan Penyebut Pecahan
a) Merasionalkan bentuk
Cara merasionalkan:
>>
b) Merasionalkan bentuk
Cara merasionalkan:
>>
>>
c) Merasionalkan bentuk
Cara merasionalkan:
>>
>>
8. Hubungan antara Pangkat Pecahan dengan Bentuk Akar
>>
>>
>>
9. Persamaan Eksponen
Jika a Є R , a ≠ 0 , maka berlaku hubungan:
>>
Sumber http://gurumatiksma.blogspot.com
0 Response to "Bentuk Pangkat, Akar Dan Logaritma"
Posting Komentar